What algorithm for a tic-tac-toe game can I use to determine the "best move" for the AI?

The Game

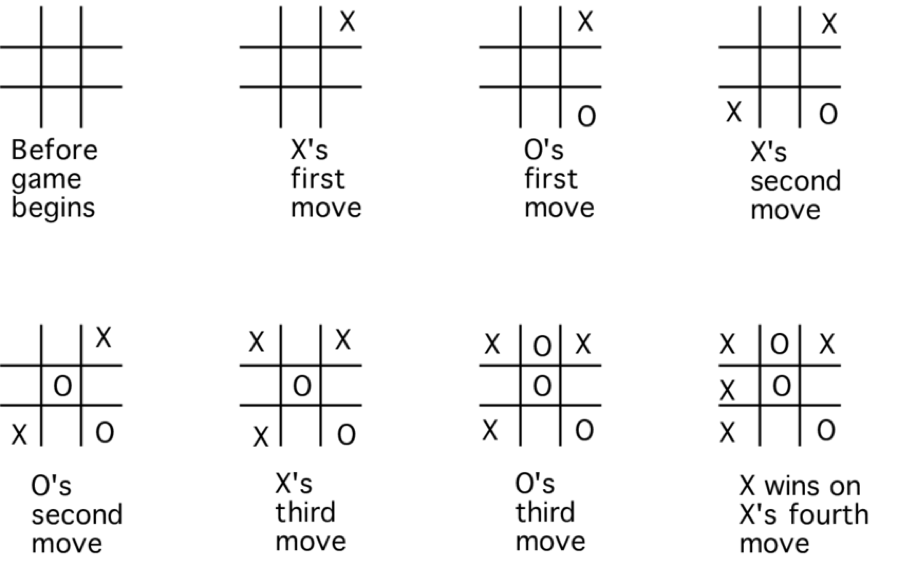
Tic-tac-toe is a very popular game for two players, X and O, who take turns marking the spaces in a 3×3 grid. The player who succeeds in placing three of their marks in a vertical, horizontal or diagonal row wins the game.

Mathematical Properties

From a mathematical point of view the game has two very important properties:

Property 1:
The game admits the player that uses this optimal strategy will win or draw but it will not lose.

Property 2:
The number of possible different matches is relatively small.

At the start, the first player can mark any of the 9 spaces. In the following turn the second player can mark one of the remaining 8 spaces and so on. The game continues until all the spaces are marked or one of the players win.

It is then easy to understand that the total number of different matches is lower than:

987....1 = 9! = 362880

That is a reasonably small number for a computer.

The Algorithm

From properties 1 and 2 it follows that a practical, and general, algorithm to win/draw the game is to use the Alpha Beta search.

At each turn the algorithm evaluates all the possible consequences of each move (possible due to property 2) and chooses the one that will ensure a victory or a draw (possible due to property 1).

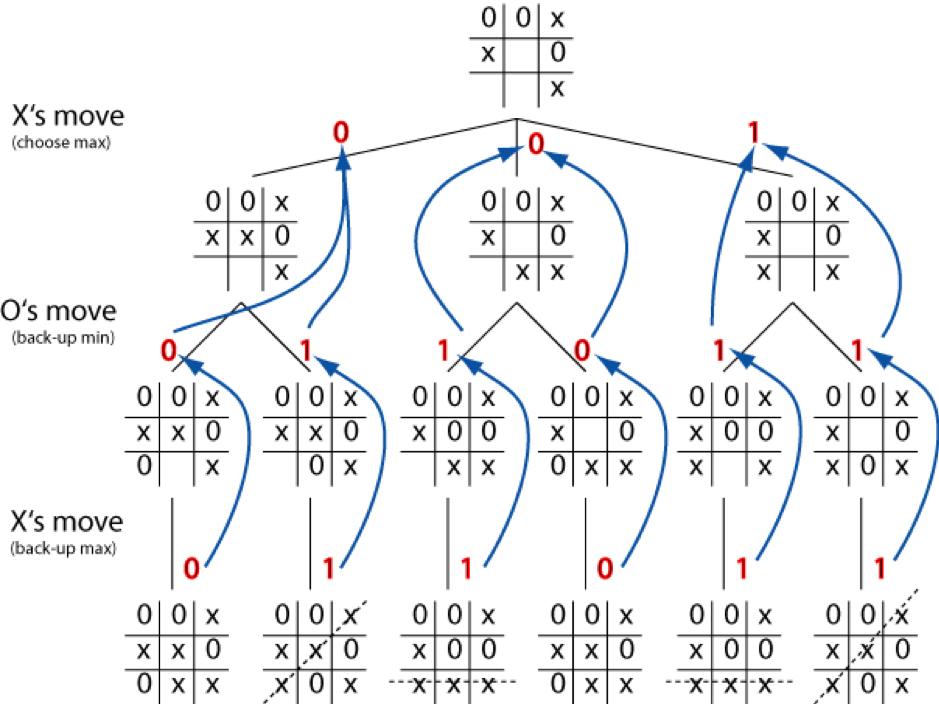
An AI player that chooses each move with the alpha beta search algorithm will never lose. To make the game more realistic it is nice to introduce a stochastic factor so that each time with a predefined probability the AI player moves randomly rather than following the alpha beta algorithm. This will make the game more realistic as it will make the AI player more human and sometimes it will lose.