What is a False Positive Rate?

What is accuracy?

A False Positive Rate is an accuracy metric that can be measured on a subset of machine learning models. In order to get a reading on true accuracy of a model, it must have some notion of “ground truth”, i.e. the true state of things. Accuracy can then be directly measured by comparing the outputs of models with this ground truth. This is usually possible with supervised learning methods, where the ground truth takes the form of a set of labels that describe and define the underlying data. One such supervised learning technique is classification, where the labels are a discrete set of classes that describe individual data points. The classifier will predict the most likely class for new data based on what it has learned about historical data. Since the data is fully labeled, the predicted value can be checked against the actual label (i.e. the ground truth) to measure the accuracy of the model.

Measuring Accuracy: Classification

The accuracy of a classifier can be understood through the use of a “confusion matrix”. This matrix describes all combinatorially possible outcomes of a classification system and lays the fundamental foundations necessary to understand accuracy measurements for a classifier. In the case of a binary classifier, there are only two labels (let us call them “Normal” and “Abnormal”). The confusion matrix can then be illustrated with the following two-class system:

In binary prediction/classification terminology, there are four conditions for any given outcome:

  • True Positive
    A True Positive is the correct identification of anomalous data as such, e.g., classifying as “abnormal” data which is in fact abnormal.
  • True Negative
    A True Negative is the correct identification of data as not being anomalous, i.e. classifying as “normal” data which is in fact normal.
  • False Positive
    A False Positive is the incorrect identification of anomalous data as such, i.e. classifying as “abnormal” data which is in fact normal.
  • False Negative
    A False Negative is the incorrect identification of data as not being anomalous, i.e. classifying as “normal” data which is in fact abnormal.

Quantifying Accuracy

There are typically two main measures to consider when examining model accuracy: the True Positive Rate (TPR) and the False Positive Rate (FPR). The TPR, or “Sensitivity”, is a measure of the proportion of positive cases in the data that are correctly identified as such. It is defined in eq. 1 as the total number of correctly identified positive cases divided by the total number of positive cases (i.e. abnormal data):

Eq. 1: where TP is the number of True Positive cases and FN is the number of False Negative cases.

The FPR, or “Fall-Out”, is the proportion of negative cases incorrectly identified as positive cases in the data (i.e. the probability that false alerts will be raised). It is defined in eq. 2 as the total number of negative cases incorrectly identified as positive cases divided by the total number of negative cases (i.e. normal data):

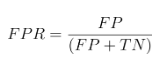
Eq. 2: where FP is the number of False Positive cases and TN is the number of True Negative cases.

Other metrics can be used to give similar views on the data:

  • The True Negative Rate, or “Specificity”, is simply 1 minus the FPR.
  • The False Negative Rate, or “Miss Rate”, is simply 1 minus the TPR.
  • The F1 Score is defined by:
Eq. 3
  • The Accuracy is defined by:
Eq. 4